type
status
category
date
slug
summary
tags
icon
Last edited time
May 21, 2023 07:57 AM
源起
程心和艾AA正要坐火箭逃亡,遇到一群小孩子,程心圣母心泛滥,要带三个小孩走,只能带三个,艾AA提出出三个问题,回答正确的可以走。
问题一
问题一:有一盖灯,关着,一分钟时闪亮了一下,再过半分钟又闪亮一下,再过十五秒再闪亮一下,以后就这样每过前面间隔时间的一半就闪亮一下,请问到两分钟时灯闪亮了多少次?答案:无数次。
解答一
这答案只能是无数次。
,求和到都无法超过,以此类推,甚至到不了两分钟,灯会亮无数次。
问题二
问题二:一根粗细不均匀的绳子,从一头点燃后烧完要用一个小时,如何用它来做15分钟的计时?注意,不均匀!
解答二
答案是绳子对折后从两头烧,那么为什么是这个答案呢?
这题的前提是火焰燃烧时,不管是哪一时刻开始点燃哪一个位置,那个位置燃烧速度是不变的。相当于就是,火焰点燃烧了无穷小的时间就熄灭,下一个无穷小的时间又开始被燃烧,火源一直不变,变的是绳子的粗细。不然考虑如果火焰越烧越旺,导致绳子越烧越快,那我感觉可能没法求解吧?
得到30min计时
先将绳子对折,然后从绳子原本的两头烧的话,应该是能做30min的计时,这应该是比较好理解的。
设绳子一头为,另一个为,绳子长记为,作出一个大概的v-t图。
由于绳子粗细不均匀,绳子燃烧时,每一刻的速度是一直在变化的,大概可以表述为:
即每一秒,每一毫秒,每一微秒······,速度都在变化,这种问题适合利用微积分解决。
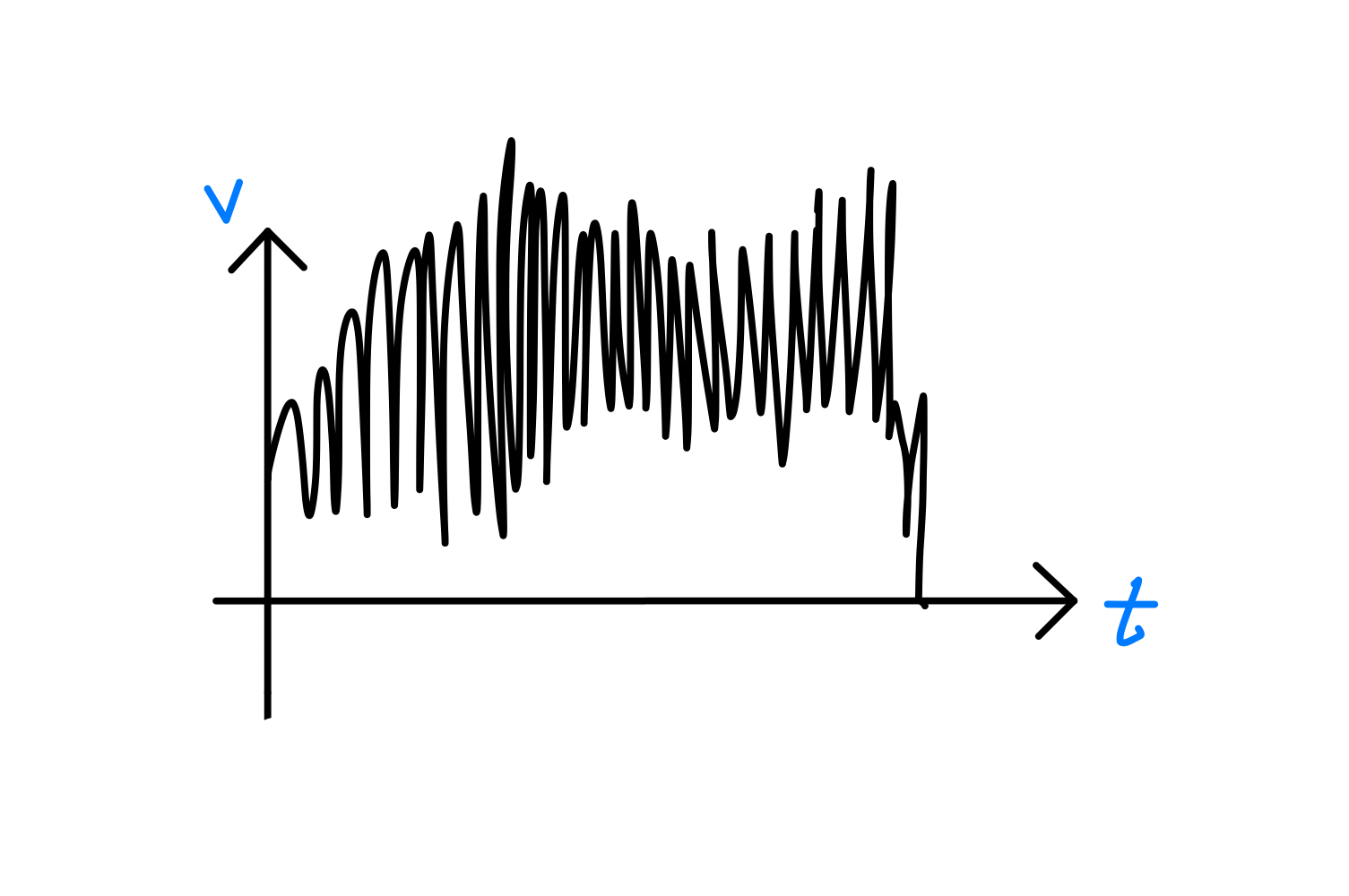
为了更直观些,将图像简化,更容易理解:
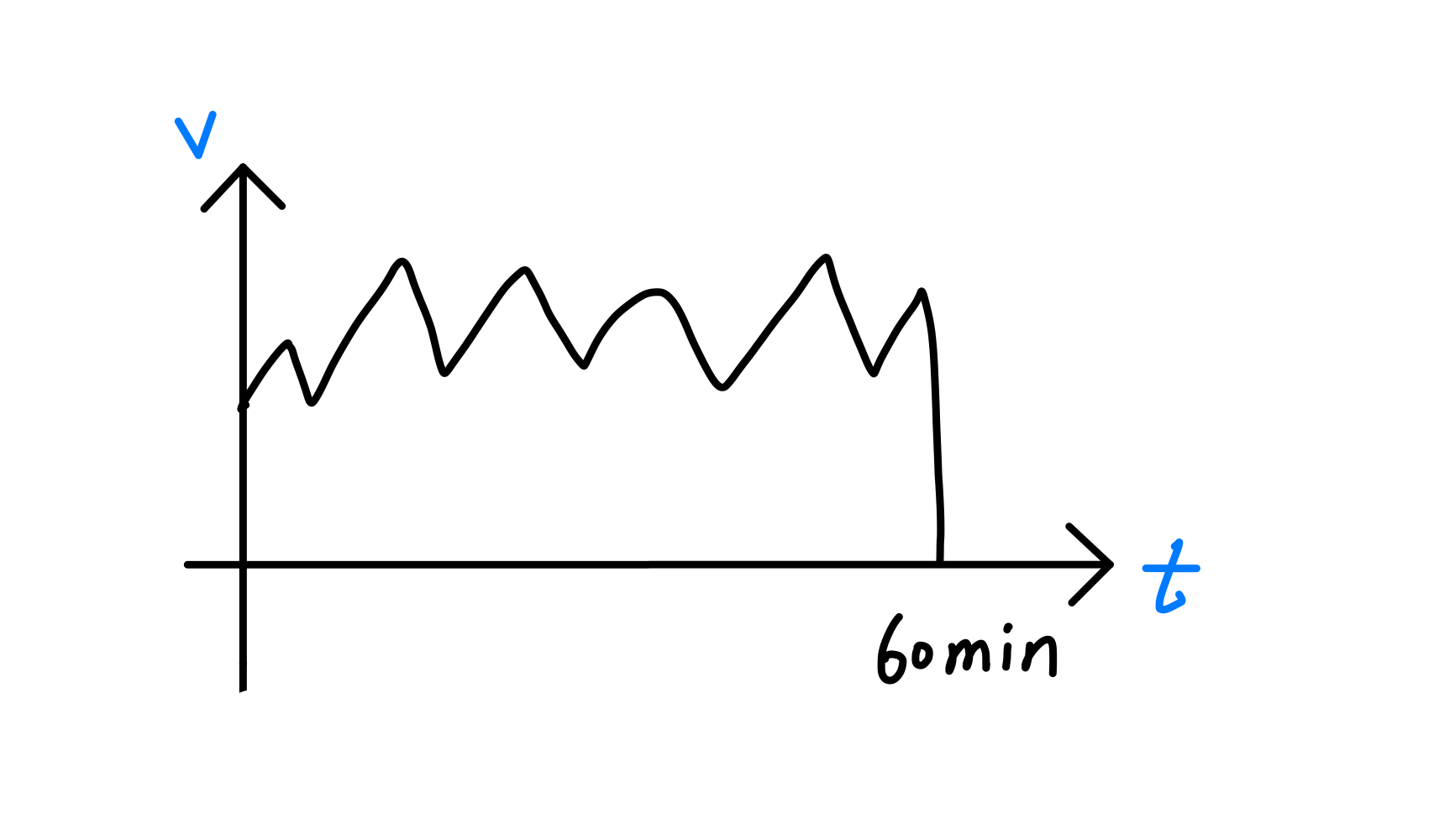
围成的面积(积分)就是绳子的长度。
从左往右积分,相当于从绳子端点燃,烧到端,函数记为,时间为60min。
从右往左积分,相当于从绳子端点燃,烧到端,函数记为,时间为60min。
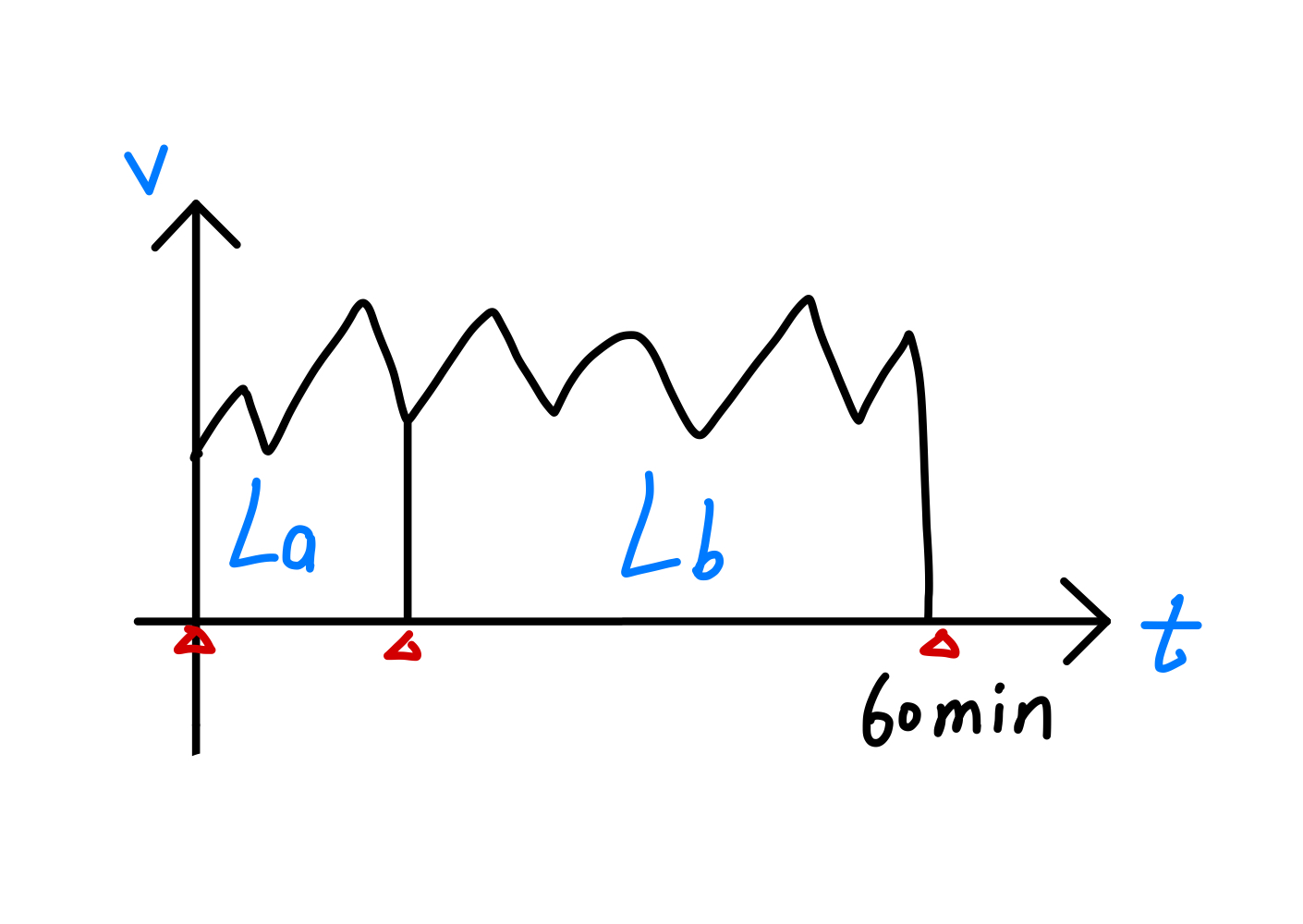
假设绳子端从0时刻开始点燃,时间为30min,则围成面积(积分)为,
绳子端从0时刻开始点燃,时间为30min,则围成面积(积分)为。
即
故
换言之,相当于从图像两端”同时向中心积分“,当积分总面积达到时,时间为30min。
我们可以得到一个结论:将绳子的两端同时点燃,燃烧完成的时间是从绳子任意一端点燃的燃烧时间的一半。
所以30min的计时是容易得到的。
那么该怎么得到15min的计时呢?
得到15min计时的一条特解
其实做法是类似的,就是把和单独看成一个,不就同理可得了吗?
- 把也从的两端“同时向中心积分”,就可以得到的燃烧时间的一半:15min
- 把也从的两端“同时向中心积分”,就可以得到的燃烧时间的一半:15min
且1,2是同时进行的,所以问题就是同时点燃3个点:
- 的左端,也就是端
- 的右端,也就是b端
- 的右端 == 的左端,实质上是同一个点
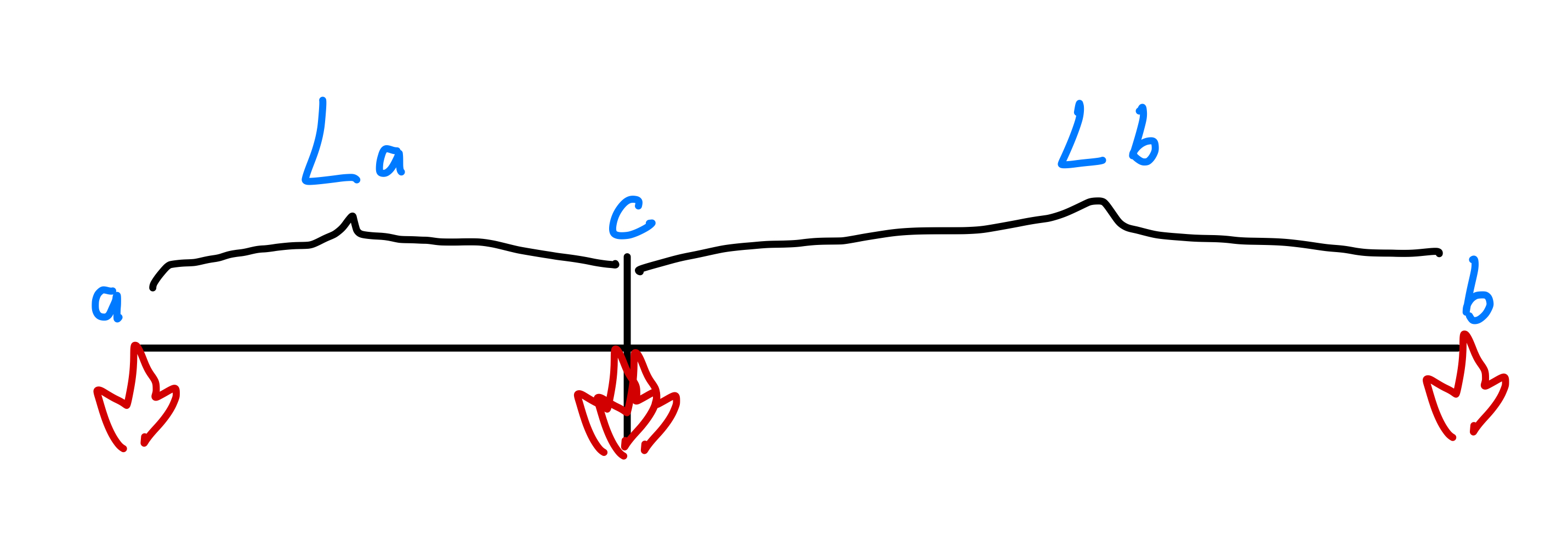
只要在或者同时点燃绳子,我们就能得到15min的计时。
问题出现
这样看似问题解决了,但是这个前提是我们能找到点,这个点是在,进行30min的积分时所得出的,实际操作并不能找到点到底在绳子的哪一个位置。
其实是可以的,如果给我们三根长短粗细完全一模一样的绳子, 我们从0时刻开始,同时点燃绳两端,绳左端 当绳烧完的时候,时间为30min,此时绳正好烧到了点 我们将绳剩余长度和绳一比较,然后把绳从点剪开,我们就得到了两段可以用于15min计时的绳子了。 把绳两段绳子的任意一段,同时从它的两端开始烧,就可以得到15min计时。 但是题目给的是一根绳子,如果是三根就可以了。
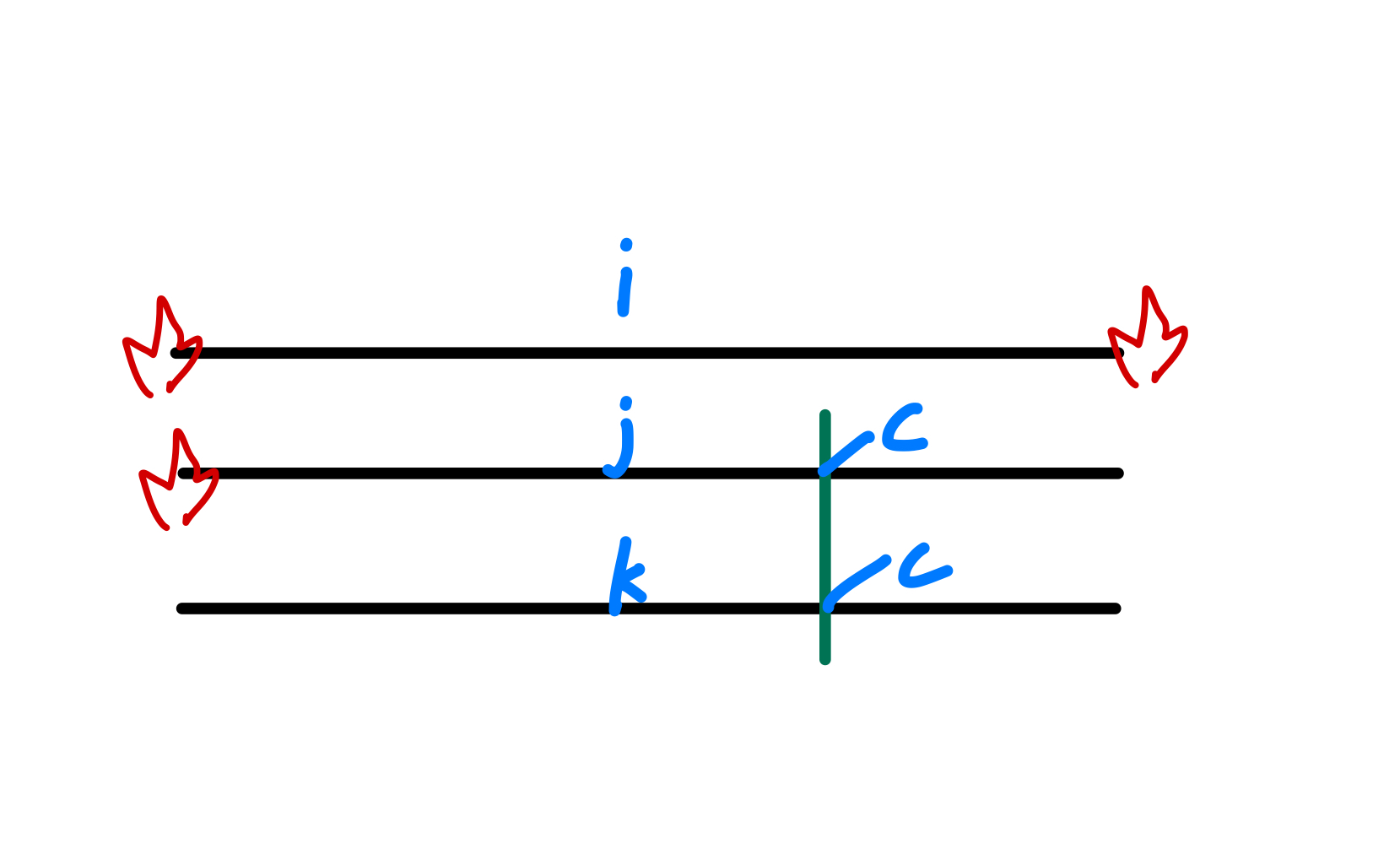
15min计时的正确求解方式
实在想不通,为什么从绳子对折一半,同时点燃两端/4个点就可以得出15min的计时。
上知乎查了查,大部分人认同的说法是这样的:

其中一根烧完了,还需要从另一根中间再点着,保证4个点在燃烧才行。
行吧,可能是三体中的答案:绳子对折后从两头烧不太严谨
问题三
问题三:82、50、26,下一个数是什么?
解答三
明显的小学题目找规律。
设下一个数为
- 作者:Jimmy Huang
- 链接:https://huangjihao.com/32b0a756-b476-4ad8-bc45-711bc0397ba0
- 声明:本文采用 CC BY-NC-SA 4.0 许可协议,转载请注明出处。