type
status
category
date
slug
summary
tags
icon
Last edited time
May 21, 2023 07:57 AM
写在前面
这是一种能够大大减少指数运算的计算资源开销的算法,在RSA这种指数非常大的加解密中很常用。
引入
指数运算最直接的方法是什么?
应该是:
*表示平方,表示乘法
这种运算方法是及其低效的。
在RSA中,指数的选择大多是在1024到3072位之间,甚至更大,以上面这种方式,则开销很大。
平方—乘算法的引入
计算需要多少次乘法?
一共需要7次乘法和平方。
有一种更快的替换方法;
一共需要3次平方。
这种方法很实用,但它只适用于幂指数为2的运算。
将这种思想进行推广,则得到了平方—乘算法
平方—乘算法引入
先通过一个例题来了解一下平方—乘算法
计算
1、先将的指数表示成二进制
2、从左到右依次扫描指数的二进制位进行计算
<table style="border-collapse: collapse; width: 100%; height: 480px;">
<tbody>
<tr style="height: 24px;">
<td style="width: 33.3333%; height: 24px;">步骤</td>
<td style="width: 33.3333%; height: 24px;"></td>
<td style="width: 33.3333%; height: 24px;">描述</td>
</tr>
<tr style="height: 48px;">
<td style="width: 33.3333%; height: 48px;">#0</td>
<td style="width: 33.3333%; height: 48px;">[latex]x=x^{{1}_2}[/latex]</td>
<td style="width: 33.3333%; height: 48px;">初始化,处理的位为:[latex]h_4[/latex] =1</td>
</tr>
<tr style="height: 72px;">
<td style="width: 33.3333%; height: 72px;">#1a</td>
<td style="width: 33.3333%; height: 72px;"> latex^2 = x^2=x^{{10}_2}[/latex]</td>
<td style="width: 33.3333%; height: 72px;">SQ,处理的位为:[latex]h_3[/latex]</td>
</tr>
<tr style="height: 48px;">
<td style="width: 33.3333%; height: 48px;">#1b</td>
<td style="width: 33.3333%; height: 48px;"> [latex]x^2\cdot x=x^3=x^{{10}_2}x^{{1}_2}=x^{{11}_2}[/latex]</td>
<td style="width: 33.3333%; height: 48px;">MUL,因为[latex]h_3[/latex] =1</td>
</tr>
<tr style="height: 48px;">
<td style="width: 33.3333%; height: 48px;">#2a</td>
<td style="width: 33.3333%; height: 48px;"> latex^2=x^6=(x^{{11}_2})^2=x^{{110}_2}[/latex]</td>
<td style="width: 33.3333%; height: 48px;">SQ,处理的位为:[latex]h_2[/latex]</td>
</tr>
<tr style="height: 48px;">
<td style="width: 33.3333%; height: 48px;">#2b</td>
<td style="width: 33.3333%; height: 48px;"></td>
<td style="width: 33.3333%; height: 48px;">没有MUL,因为[latex]h_2[/latex] =0</td>
</tr>
<tr style="height: 48px;">
<td style="width: 33.3333%; height: 48px;">#3a</td>
<td style="width: 33.3333%; height: 48px;"> latex^2=x^{12} = (x^{{110}_2})^2=x^{{1100}_2}[/latex]</td>
<td style="width: 33.3333%; height: 48px;">SQ,处理的位为:[latex]h_1[/latex]</td>
</tr>
<tr style="height: 48px;">
<td style="width: 33.3333%; height: 48px;">#3b</td>
<td style="width: 33.3333%; height: 48px;"> [latex]x^{12}\cdot x=x^{13}=x^{{1100}_2}x^{{1}_2}=x^{{1101}_2}[/latex]</td>
<td style="width: 33.3333%; height: 48px;">MUL,因为[latex]h_1[/latex] =1</td>
</tr>
<tr style="height: 48px;">
<td style="width: 33.3333%; height: 48px;">#4a</td>
<td style="width: 33.3333%; height: 48px;"> latex^2=x^{26}=(x^{{1101}_2})^2=x^{{11010}_2}[/latex]</td>
<td style="width: 33.3333%; height: 48px;">SQ,处理的位为:[latex]h_0[/latex]</td>
</tr>
<tr style="height: 48px;">
<td style="width: 33.3333%; height: 48px;">#4b</td>
<td style="width: 33.3333%; height: 48px;"></td>
<td style="width: 33.3333%; height: 48px;">MUL,因为[latex]h_0[/latex] =0</td>
</tr>
</tbody>
</table>
步骤
描述
[latex]x^{12}\cdot x=x^{13}=x^{{1100}_2}x^{{1}_2}=x^{{1101}_2}[/latex]
MUL,因为[latex]h_1[/latex] =1
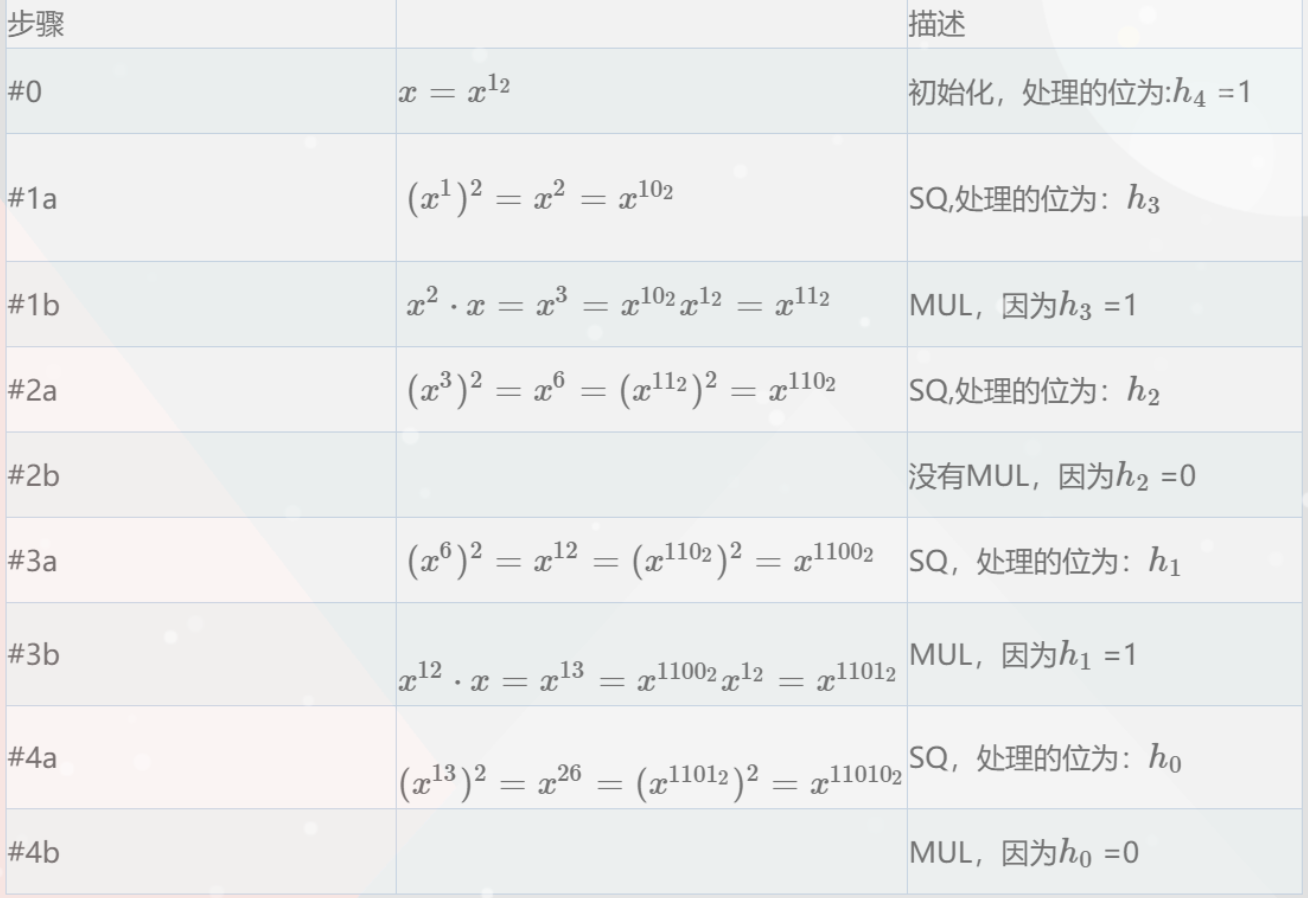
明白了这个算法的过程了吗?
这里来解释一下:
第0步是初始化的,得到
后面每一步分为a、b两步
a步是必走的 做平方
b步取决于指数二进制位数的值,如果是1,则做乘法,如果是0则不需要
这种方式则可以计算所有指数的指数运算了,并且相当的高效。
代码实现
Python实现
C实现
*也挺简单的,我就不写了(懒
参考资料
Understanding Cryptography: A Textbook for Students and Practitioners
- 作者:Jimmy Huang
- 链接:https://huangjihao.com/d465fee6-cb21-4706-b251-4c72347507c2
- 声明:本文采用 CC BY-NC-SA 4.0 许可协议,转载请注明出处。